Часть 1
Часть 2
Часть 3
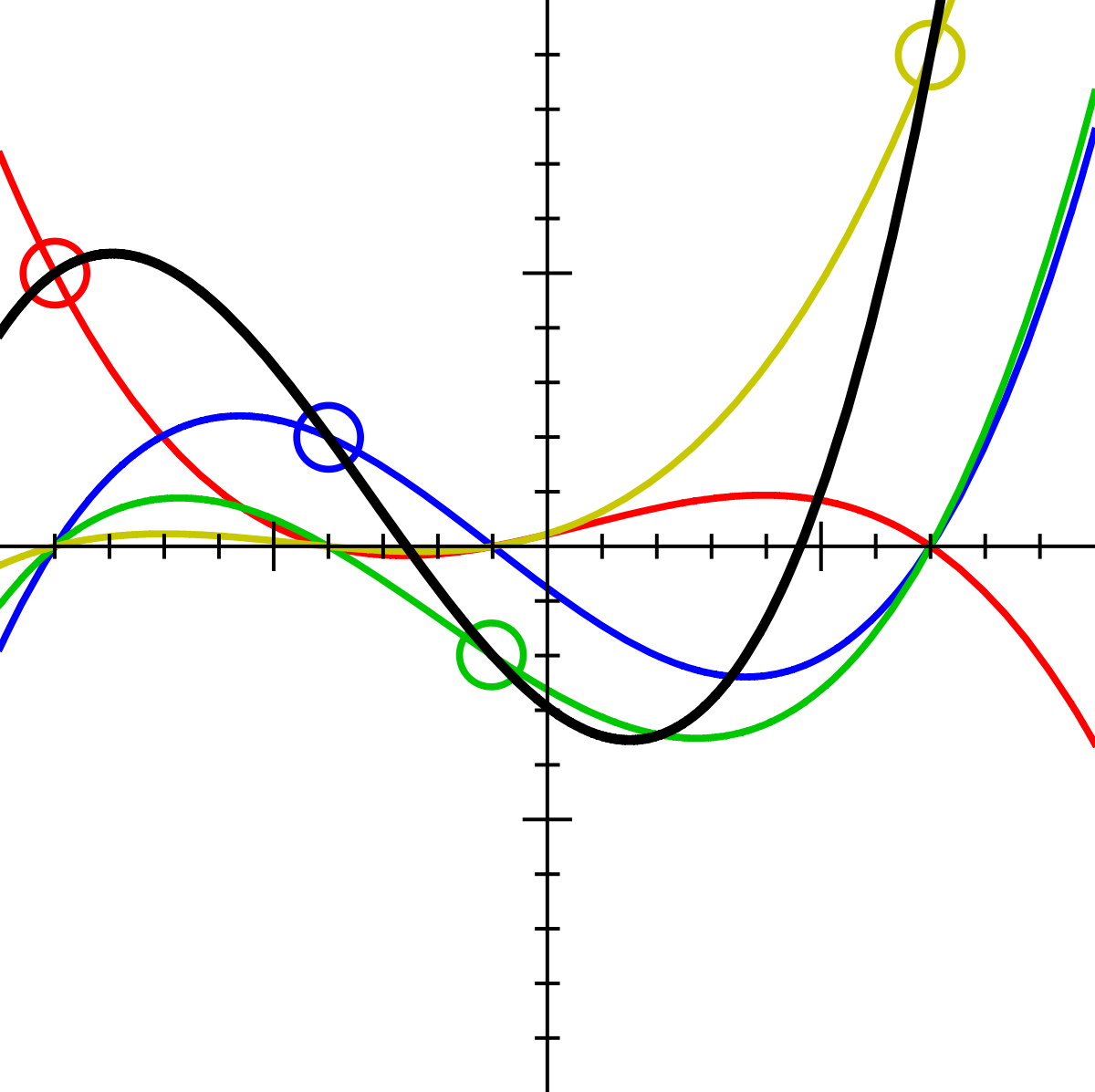
Вот бывает решаешь такой квадратное уравнение, в нем оказывается отрицательный дискриминант и ты такой: еее, не надо досчитывать. А теперь ты знаешь, что бывают комплексные числа и можно извлечь квадратный корень из отрицательных чисел, то есть у квадратного уравнения всегда есть корень в комплексных числах. На самом деле верен и куда более общий факт: у любого многочлена с комплексными (в частности, с действительными) коэффициентами есть корень в комплексных числах. Это утверждение называется основной теоремой алгебры. На самом деле в современной алгебре она уже не играет сильно большой роли, но название осталось со времен, когда основной задачей алгебры было нахождение корней многочленов.
На самом деле эта теорема показывает, насколько круты комплексные числа, потому что оказывается в них можно найти корень у любого многочлена.
Одним из первых строгое доказательство этой теоремы дал "король математиков" Карл Гаусс (вообще говоря, за всю жизнь Гаусс дал 5 различных доказательств этой теоремы), но для понятия его доказательства нужна некоторая математическая сноровка, так что мы докажем ее по-другому, с применением математического анализа (без одной леммы, которую примем на веру).
Лемма 1. Помните, что такое модуль комплексного числа? Так вот, если мы посчитаем модуль у комплексного числа w = f(z), то полученная функция (|f(z)|) будет непрерывной, то есть функция не будет разрываться, не будет бешено скакать и нигде не будет улетать на бесконечность (в конечных точках имеется в виду) и так далее. Доказательство очевидно: многочлен - непрерывная функция, модуль тоже, значит модуль от многочлена тоже непрерывная функция.
Лемма 2. Существует замкнутый (то есть с границей) кружок конечного радиуса (помните, у нас комплексные числа – они как точки на плоскости), в котором функция не улетает на бесконечность. Ну так это ж следует из предыдущей леммы.
Лемма 3. Непрерывная функция достигает своего минимума в замкнутом кружочке. Не буду томить, скажу, что это теорема Вейерштрасса и ее можно доказать очень просто: возьмем последовательность точек, значения которых сходятся к минимуму. Поскольку функция непрерывна, они сходятся к какой-то точке, значение в которой равно пределу значений этих точек. Но их значения сходятся к минимуму, значит, будет точка, в которой значение минимально.
Итак, мы доказали, что есть кружочек, в котором функция достигает своего минимума. Осталось показать, что значение этого минимума равно нулю. Можно показать, что если он не ноль, то есть значение ещё меньше. Это на самом деле сложный факт и доказывать я его не буду, это долго и непонятно.
Таким образом, используя все эти леммы получаем, что есть кружок, в котором достигается минимум, если он не ноль, значит где-то он меньше, а значит, мы нашли не минимум. Противоречие.
Данное доказательство использует лемму д'Аламбера, которая доказывается не очень сложно, но уж больно муторно. Этот вариант доказательства является наиболее простым и его можно встретить в любом учебнике по алгебре.
Только вот возникает ряд проблем – доказательство совершенно не имеет ничего общего с алгеброй. В действительности мы использовали только матанализ и свойства комплексных чисел. Вторая проблема – абсолютная бесполезность (на первый взгляд) этой теоремы. Ну правда, она говорит лишь о том, что корни существуют, она даже не дает алгоритма поиска. То есть мы не сможем решить даже приблизительно. Третья проблема – отсутствие глубинного математического смысла. Она абсолютно не отражает свойства поля комплексных чисел, как структуры. Даже недоказанная лемма д'Аламбера ничего такого не даёт.
Тем не менее само наличие корня любого многочлена является потрясающим фактом и помогает повсеместно – в линейной алгебре, матанализе, теории чисел, дифференциальных уравнениях и так далее (хотя, скорее, это универсальность многочленов, а не этой теоремы).
Спасибо за то, что вы с нами.
С любовью, Рителлинг favorite