Напомню, что n! = n*(n-1)*(n-2)*...*3*2*1
Примеры:
4! = 4 * 3 * 2 * 1 = 24
5! = 5 * 4 * 3 * 2 * 1 = 5 * 4! = 120
При этом нам необходимо, чтобы на целых числах всё осталось как было. Иными словами, если и получилось у нас что-то новое, то оно хорошо согласуется с тем, что уже имеется. Ну и естественно хотелось бы придумать такое обобщение, чтобы не было какой-нибудь фигни типа 3! = 6; 4! = 24; а (3,5)! = -200. Это было бы очень странно и неестественно. Также хочется, чтобы полученное обобщение можно было как-то нормально считать, хотя бы приблизительно, то есть чтобы не было чего-то типа "ну мы продолжили по непрерывности, а дальше считайте как хотите", такой способ подсчета нас не устроит. Еще хотелось бы, чтобы функция была плавная. Например, самое простое, что хочется сделать, это просто продолжить линейно, отрезками:

Но тут возникает проблема – график не плавный, у него изломы во всех целых точках. Да, конечно, при больших числах это уже не так заметно, но если мы хотим посчитать что-то при маленьких значениях переменной, то всё плохо.
Итак, данный вопрос вставал перед Эйлером и он не мудрствуя лукаво решил определить обобщение факториала тоже через произведение, только не конечное, а бесконечное. В общем, тут схожести и заканчиваются, потому что в определении Эйлера нет никаких умножений на предыдущее число, а сама формула выглядит жутко и непонятно:

Тут большая буква П означает произведение, но в общем не берите в голову, все равно ничего понятно.
В общем Эйлер придумал такую функцию и использовал ее для своих нужд.
Более удобное определение можно дать в качестве такого интеграла с параметром:

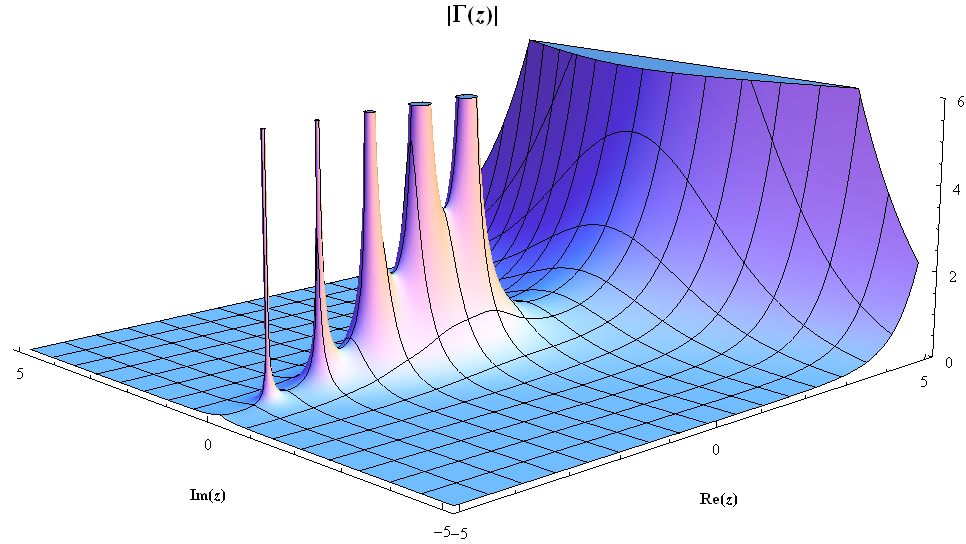
Данный интеграл определяется для числа z и для каждого z выдает число, которое и называется гамма-функцией.