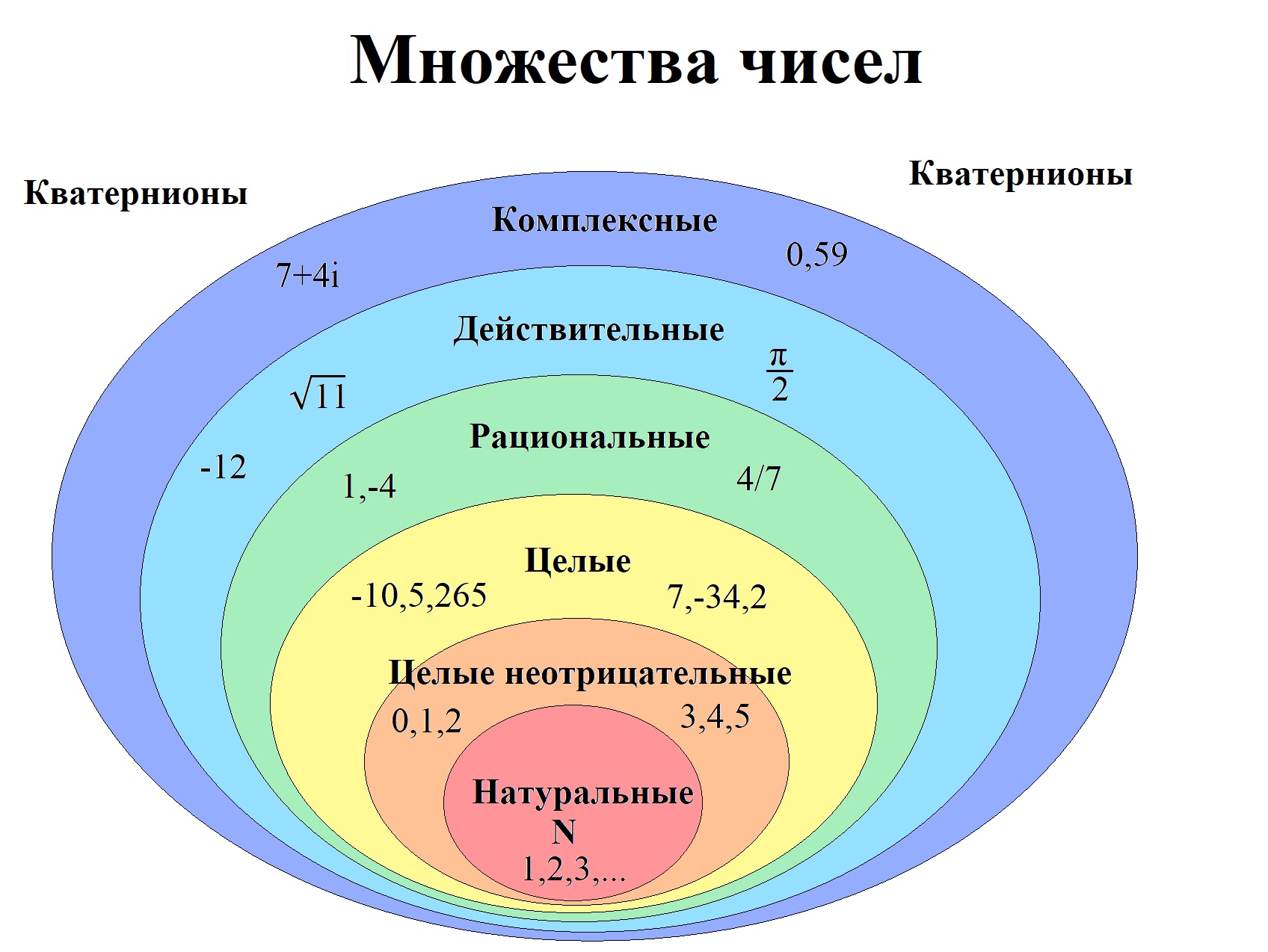
Множество - это совокупность каких-либо объектов, у которых между собой есть что-то общее (они будут объединены по какому-то признаку). Среди очевидных примеров будет множество рабочих на заводе, чаинок в твоем чае или звезд на небе. Записывается это примерно так: x∈X (где x - элемент, X - соответствующего ему множества) или х∉Х (в данном случае элемент не принадлежит нужному множеству).
Также существует и пустое множество в котором нет ничего. Поэтому оно и пустое :) Обозначают символом - ∅
А теперь об интересном. Множество А (полосатых котиков) называют подмножеством множества В (котиков), если каждый элемент множества А является элементом множества В. То есть, все полосатые котики должны быть котиками. Множества состоящие из одних и тех же элементов будут называться равными. Изученных операций над множествами существует 4 (насколько я знаю). Все изображения ниже представлены на диаграммах Эйлера-Венна.
1. Пересечение — множество, элементы которого принадлежат и первому, и второму множеству одновременно

2. Объединение — множество, элементы которого принадлежат хотя бы одному из множеств.

3. Разность —множество, элементы которого принадлежат только множеству А

4. Симметрическая разность — множество, элементы которого принадлежат одному из множеств.

Любое множество может быть подмножеством универсального множества (в нём будут содержаться все множества, объекты и элементы)
Ну и на последок остается вопрос «на подумать»: может ли множество быть подмножеством самого себя?